打了场CF，来写个题解吧，第一次写题解好鸡冻。
C. Vladik and fractions
time limit per test
1 secondmemory limit per test
256 megabytesinput
standard inputoutput
standard outputVladik and Chloe decided to determine who of them is better at math. Vladik claimed that for any positive integer n he can represent fraction 
as a sum of three distinct positive fractions in form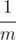 
.
Help Vladik with that, i.e for a given n find three distinct positive integers x, y and z such that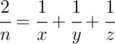 
. Because Chloe can't check Vladik's answer if the numbers are large, he asks you to print numbers not exceeding 109.
If there is no such answer, print -1.
Input
The single line contains single integer n (1 ≤ n ≤ 104).
Output
If the answer exists, print 3 distinct numbers x, y and z (1 ≤ x, y, z ≤ 109, x ≠ y, x ≠ z, y ≠ z). Otherwise print -1.
If there are multiple answers, print any of them.
Examples
Input
3
Output
2 7 42
Input
7
Output
7 8 56
让你分解 这个数。
本来看了题面打算写个dfs按照分解出来的因数搜索一下解，然而怎么想都觉得很奇怪，然后火神Q我说仔细看第二组样例这才做出了这道SB题。$n==1$ 的时候输出无解，其他都可以直接输出
第二组样例：
input
7
output
7 8 56
代码
#pragma comment(linker, "/STACK:1024000000,1024000000")
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#include<set>
#include<queue>
#include<map>
#include<string>
#include<cmath>
#include<cstdlib>
#include<ctime>
using namespace std;
typedef long long ll;
ll gcd(ll a, ll b)
{
return b == 0 ? a : gcd(b, a % b);
}
int main()
{
ll n;
while (cin >> n)
{
if (n == 1)
cout << -1 << endl;
else
cout << n << " " << n + 1 << " " << n * (n + 1) << endl;
}
return 0;
}
D. Chloe and pleasant prizes
time limit per test2 seconds
memory limit per test256 megabytes
inputstandard input
outputstandard output
>Generous sponsors of the olympiad in which Chloe and Vladik took part allowed all the participants to choose a prize for them on their own. Christmas is coming, so sponsors decided to decorate the Christmas tree with their prizes.
>They took n prizes for the contestants and wrote on each of them a unique id (integer from 1 to n). A gift i is characterized by integer ai — pleasantness of the gift. The pleasantness of the gift can be positive, negative or zero. Sponsors placed the gift 1 on the top of the tree. All the other gifts hung on a rope tied to some other gift so that each gift hung on the first gift, possibly with a sequence of ropes and another gifts. Formally, the gifts formed a rooted tree with n vertices.
>
>The prize-giving procedure goes in the following way: the participants come to the tree one after another, choose any of the remaining gifts and cut the rope this prize hang on. Note that all the ropes which were used to hang other prizes on the chosen one are not cut. So the contestant gets the chosen gift as well as the all the gifts that hang on it, possibly with a sequence of ropes and another gifts.
>
>Our friends, Chloe and Vladik, shared the first place on the olympiad and they will choose prizes at the same time! To keep themselves from fighting, they decided to choose two different gifts so that the sets of the gifts that hang on them with a sequence of ropes and another gifts don't intersect. In other words, there shouldn't be any gift that hang both on the gift chosen by Chloe and on the gift chosen by Vladik. From all of the possible variants they will choose such pair of prizes that the sum of pleasantness of all the gifts that they will take after cutting the ropes is as large as possible.
>
>Print the maximum sum of pleasantness that Vladik and Chloe can get. If it is impossible for them to choose the gifts without fighting, print Impossible.
>Input
The first line contains a single integer n (1 ≤ n ≤ 2·105) — the number of gifts.
>The next line contains n integers a1, a2, ..., an ( - 109 ≤ ai ≤ 109) — the pleasantness of the gifts.
>The next (n - 1) lines contain two numbers each. The i-th of these lines contains integers ui and vi (1 ≤ ui, vi ≤ n, ui ≠ vi) — the description of the tree's edges. It means that gifts with numbers ui and vi are connected to each other with a rope. The gifts' ids in the description of the ropes can be given in arbirtary order: vi hangs on ui or ui hangs on vi.
>It is guaranteed that all the gifts hang on the first gift, possibly with a sequence of ropes and another gifts.
>Output
>If it is possible for Chloe and Vladik to choose prizes without fighting, print single integer — the maximum possible sum of pleasantness they can get together.
>Otherwise print Impossible.
题意就是让从一棵树上选两个相互独立的子树，使得被选取的节点的和最大。
直接从根节点dfs一遍就可以得到：
- 取以当前节点为根的子树的和
- 在当前节点及以下取一颗树的最大和
- 在当前节点以下取两棵树的最大和
其中第三点可以由一二两个值得到，那么递归到根节点就可以了。
代码
#pragma comment(linker, "/STACK:1024000000,1024000000")
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#include<set>
#include<queue>
#include<map>
#include<string>
#include<cmath>
#include<cstdlib>
#include<ctime>
using namespace std;
const int maxn = 200000 + 100;
vector<int> G[maxn];
typedef long long ll;
ll a[maxn];
ll dp[maxn];
const ll inf = 0x3f3f3f3f3f3f3f3f;
void add_edge(int u, int v)
{
G[u].push_back(v);
G[v].push_back(u);
}
ll dfs1(int u, int p)
{
ll mm = -inf;
ll sum = 0;
for (int i = 0; i < G[u].size(); i++)
{
if (G[u][i] != p)
{
ll tmp = dfs1(G[u][i], u);
mm = max(mm, dp[G[u][i]]);
sum += tmp;
}
}
//cout << u << " " << max(a[u] + sum, mm) << endl;
dp[u] = max(a[u] + sum, mm );
return sum + a[u];
}
ll dfs2(int u, int p)
{
ll prem = -inf, mm = -inf;
for (int i = 0; i < G[u].size(); i++)
{
if (G[u][i] != p)
{
if (mm < dp[G[u][i]])
{
prem = mm;
mm = dp[G[u][i]];
}
else if (prem < dp[G[u][i]])
{
prem = dp[G[u][i]];
}
}
}
ll ans = prem + mm;
for (int i = 0; i < G[u].size(); i++)
{
if (G[u][i] != p)
{
ans = max(ans, dfs2(G[u][i], u));
}
}
return ans;
}
int main()
{
ll n;
while (cin >> n)
{
for (int i = 0; i < n; i++)
{
cin >> a[i];
}
for (int i = 0; i < n; i++)
{
G[i].clear();
}
int u, v;
for (int i = 1; i < n; i++)
{
cin >> u >> v;
add_edge(u - 1, v - 1);
}
dfs1(0, -1);
ll ans = dfs2(0, -1);
if (ans < -inf / 2)
{
cout << "Impossible\n";
}
else
{
cout << ans << endl;
}
}
return 0;
}
/*
4
-1
*/